Để học tốt Giải tích 12, phần này giúp bạn giải các bài tập trong sách giáo khoa Toán 12 được biên soạn bám sát theo nội dung sách Giải tích 12. Dưới đây chúng ta sẽ cùng tìm hiểu nội dung Cực Trị Của Hàm Số – Toán 12 và giải một số bài tập liên quan đến nội dung này để nắm chắc kiến thức nhé!
I. Lý thuyết Cực trị hàm số
1. Định nghĩa:
Cho hàm số y = f(x) xác định và liên tục trên khoảng (a; b) (có thể a là -∝; b là +∝) và điểm xo ∈ (a; b) .
– Nếu tồn tại số h > 0 sao cho f(x) < f(xo) với mọi x ∈ (xo – h; xo + h) và x ≠ xo thì ta nói hàm số f(x) đạt cực đại tại xo .
– Nếu tồn tại số h > 0 sao cho f(x) > f(xo) với mọi x ∈ (xo – h; xo + h) và x ≠ xo thì ta nói hàm số f(x) đạt cực tiểu tại xo .
2. Điều kiện đủ để hàm số có cực trị:
Giả sử hàm số y = f(x) liên tục trên K = (xo – h; xo + h) và có đạo hàm trên K hoặc trên K \ {xo}, với h > 0 .
– Nếu f'(x) > 0 trên khoảng (xo – h; xo) và f'(x) < 0 trên (xo; xo + h) thì xo là một điểm cực đại của hàm số f(x).
– Nếu f'(x) < 0 trên khoảng (xo – h; xo) và f'(x) > 0 trên (xo; xo + h) thì xo là một điểm cực tiểu của hàm số f(x).
Minh họa bằng bảng biến thiến

* Chú ý.
– Nếu hàm số y = f(x) đạt cực đại (cực tiểu) tại xo thì xo được gọi là điểm cực đại (điểm cực tiểu) của hàm số; f(xo) được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số, kí hiệu là fCĐ(fCT) , còn điểm M(xo; f(xo)) được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.
– Các điểm cực đại và cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.
B. Kĩ năng giải bài tập
1. Quy tắc tìm cực trị của hàm số
– Quy tắc 1:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tính f'(x) . Tìm các điểm tại đó f'(x) bằng 0 hoặc f'(x) không xác định.
Bước 3. Lập bảng biến thiên.
Bước 4. Từ bảng biến thiên suy ra các điểm cực trị.
– Quy tắc 2:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tính f'(x). Giải phương trình f'(x) và ký hiệu xi (i = 1; 2; 3;…) là các nghiệm của nó.
Bước 3. Tính f”(x) và f”(xi).
Bước 4. Dựa vào dấu của f”(xi) suy ra tính chất cực trị của điểm xi.
2. Kỹ năng giải nhanh các bài toán cực trị hàm số bậc ba y = ax3 + bx2 + cx + d (a ≠ 0)
Ta có y’= 3ax2 + 2bx + c
– Đồ thị hàm số có hai điểm cực trị khi phương trình y’ = 0 có hai nghiệm phân biệt ⇔ b2 – 3ac > 0. Khi đó đường thẳng qua hai điểm cực trị đó là : 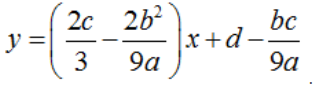 .
.
– Bấm máy tính tìm ra đường thẳng đi qua hai điểm cực trị :
![]()
Hoặc sử dụng công thức 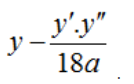 .
.
– Khoảng cách giữa hai điểm cực trị của đồ thị hàm số bậc ba là:
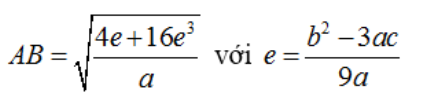
3. Kỹ năng giải nhanh các bài toán cực trị hàm trùng phương.
Cho hàm số: y = ax4 + bx2 + c (a ≠ 0) có đồ thị là (C).
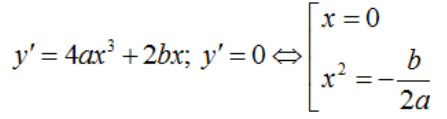
(C) có ba điểm cực trị y’ = 0 có 3 nghiệm phân biệt 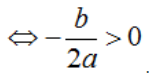 .
.
Khi đó ba điểm cực trị là:  với Δ = b2 – 4ac
với Δ = b2 – 4ac
Độ dài các đoạn thẳng: 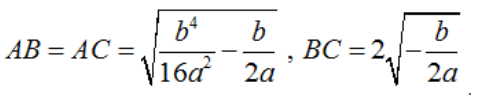 .
.
Các kết quả cần ghi nhớ:
– ΔABC vuông cân ⇔ BC2 = AB2 + AC2
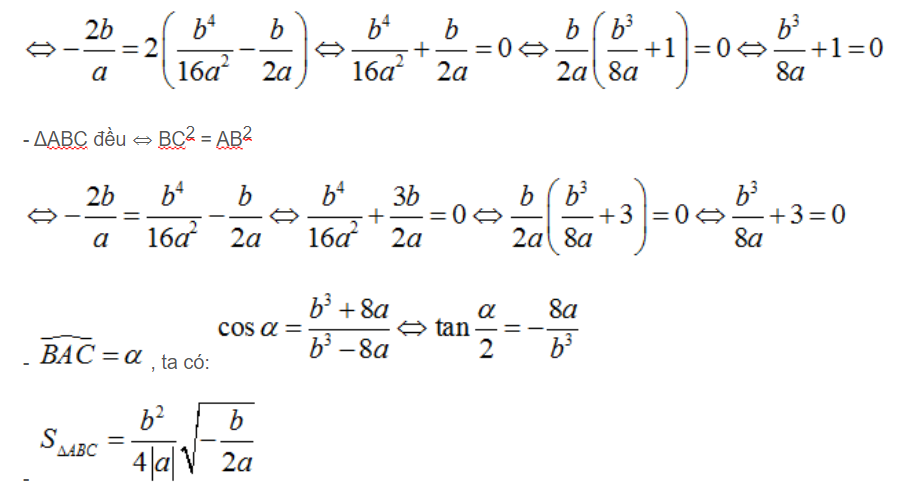
– Bán kính đường tròn ngoại tiếp ΔABC là 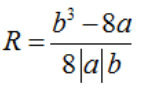
– Bán kính đường tròn nội tiếp ΔABC là 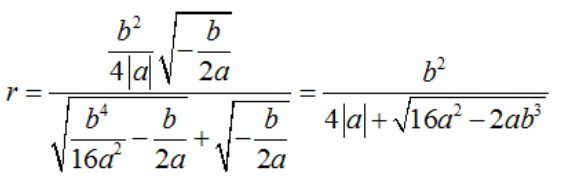
– Phương trình đường tròn ngoại tiếp ΔABC là: 
C. Kĩ năng sử dụng máy tính
Ví dụ 1: Tìm đường thẳng đi qua hai điểm cực trị của đồ thị hàm số: y = x3 + 3x2 – x + 2
Hướng dẫn:
Bấm máy tính: MODE 2
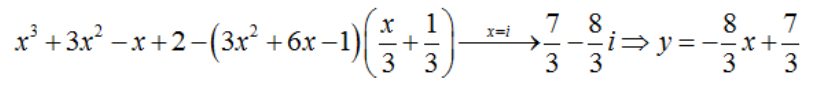
Ví dụ 2: Tìm đường thẳng đi qua hai điểm cực trị ( nếu có ) của đồ thị hàm số: y = x3 – 3x2 + m2x + m
Hướng dẫn:
Bấm máy tính: MODE 2
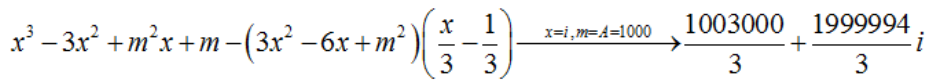
Ta có:
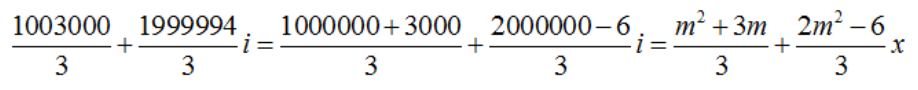
Vậy đường thẳng cần tìm:
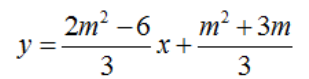
II. GIẢI BÀI TẬP SGK
Bài 1 (trang 18 SGK Giải tích 12): Áp dụng Quy tắc 1, hãy tìm các điểm cực trị của các hàm số sau:
a) y = 2x3 + 3x2 – 36x – 10
Lời giải:
a) TXĐ: D = R
y’ = 6x2 + 6x – 36
y’ = 0 ⇔ x = -3 hoặc x = 2
Bảng biến thiên:
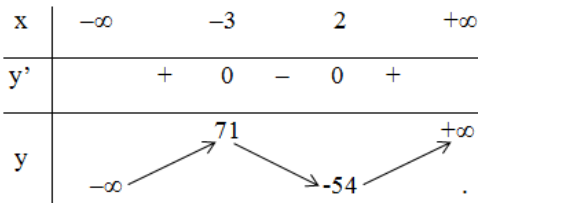
Kết luận :
Hàm số đạt cực đại tại x = -3 ; yCĐ = 71
Hàm số đạt cực tiểu tại x = 2; yCT = -54.
b) TXĐ: D = R
y’= 4x3 + 4x = 4x(x2 + 1) = 0;
y’ = 0 ⇔ x = 0
Bảng biến thiên:
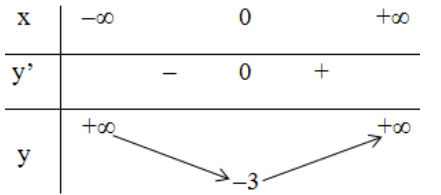
Vậy hàm số đạt cực tiểu tại x = 0; yCT = -3
hàm số không có điểm cực đại.
c) TXĐ: D = R \ {0}
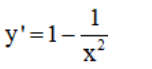
y’ = 0 ⇔ x = ±1
Bảng biến thiên:
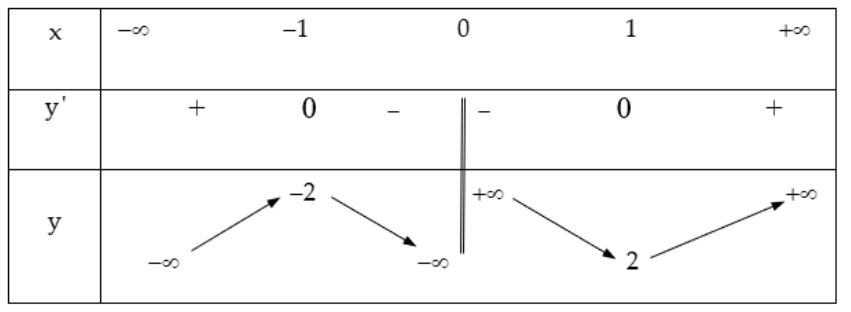
Vậy hàm số đạt cực đại tại x = -1; yCĐ = -2;
hàm số đạt cực tiểu tại x = 1; yCT = 2.
d) TXĐ: D = R
y’= (x3)’.(1 – x)2 + x3.[(1 – x)2]’
= 3x2.(1 – x)2 + x3.2(1 – x).(1 – x)’
= 3x2(1 – x)2 – 2x3(1 – x)
= x2.(1 – x)(3 – 5x)
y’ = 0 ⇔ x = 0; x = 1 hoặc x = 3/5
Bảng biến thiên:
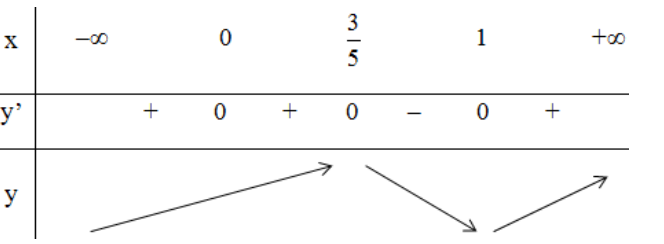
Vậy hàm số đạt cực đại tại x = ![]()
hàm số đạt cực tiểu tại xCT = 1.
(Lưu ý: x = 0 không phải là cực trị vì tại điểm đó đạo hàm bằng 0 nhưng đạo hàm không đổi dấu khi đi qua x = 0.)
e) Tập xác định: D = R.
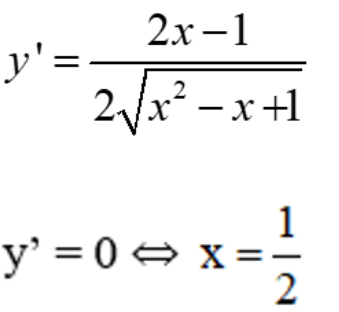
Bảng biến thiên:
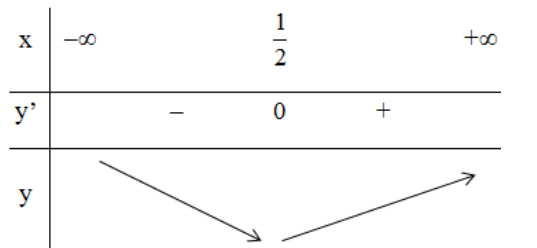
Vậy hàm số đạt cực tiểu tại x = 1/2.
Bài 2 (trang 18 SGK Giải tích 12):
Áp dụng Quy tắc 2, hãy tìm các điểm cực trị của hàm số sau:
a) y = x4 – 2x2 + 1 ;
b) y = sin2x – x
c) y = sinx + cosx ;
d) y = x5 – x3 – 2x + 1
Lời giải:
a) TXĐ: D = R.
+ y’ = 4x3 – 4x
y’ = 0 ⇔ 4x(x2 – 1) = 0 ⇔ x = 0 hoặc x = ±1.
+ y” = 12x2 – 4
y”(0) = -4 < 0 ⇒ x = 0 là điểm cực đại của hàm số.
y”(1) = 8 > 0 ⇒ x = 1 là điểm cực tiểu của hàm số.
y”(-1) = 8 > 0 ⇒ x = -1 là điểm cực tiểu của hàm số.
b) TXĐ: D = R
+ y’ = 2cos2x – 1;

+ y” = -4.sin2x
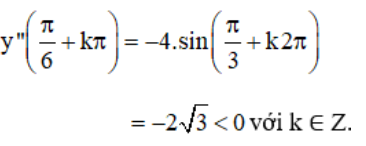
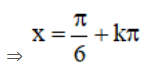 (k ∈ Z) là các điểm cực đại của hàm số.
(k ∈ Z) là các điểm cực đại của hàm số.
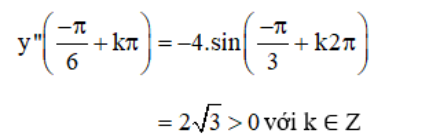
⇒ 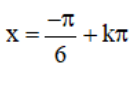 (k ∈ Z) là các điểm cực tiểu của hàm số.
(k ∈ Z) là các điểm cực tiểu của hàm số.
c) TXĐ: D = R
+ y’ = cos x – sin x.

+ y’’ = -sin x – cos x = 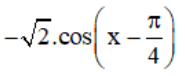
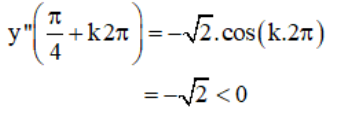
⇒  là các điểm cực đại của hàm số.
là các điểm cực đại của hàm số.
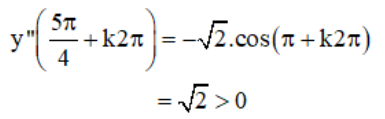
⇒ 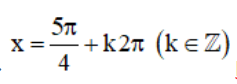 là các điểm cực tiểu của hàm số.
là các điểm cực tiểu của hàm số.
d) TXĐ: D = R
+ y’= 5x4 – 3x2 – 2
y’ = 0 ⇔ 5x4 – 3x2 – 2 = 0
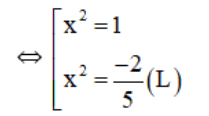
⇔ x = ±1.
+ y” = 20x3 – 6x
y”(-1) = -20 + 6 = -14 < 0
⇒ x = -1 là điểm cực đại của hàm số.
y”(1) = 20 – 6 = 14 > 0
⇒ x = 1 là điểm cực tiểu của hàm số.
Bài 3 (trang 18 SGK Giải tích 12):
Chứng minh hàm số y = √|x| không có đạo hàm tại x = 0 nhưng vẫn đạt được cực tiểu tại điểm đó.
Lời giải:
Hàm số có tập xác định D = R và liên tục trên R.
+ Chứng minh hàm số ![]() không có đạo hàm tại x = 0.
không có đạo hàm tại x = 0.
Xét giới hạn  :
:
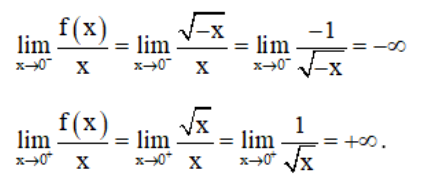
⇒ Không tồn tại giới hạn 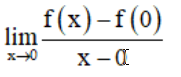
Hay hàm số không có đạo hàm tại x = 0.
+ Chứng minh hàm số đạt cực tiểu tại x = 0 (Dựa theo định nghĩa).
Ta có : f(x) > 0 = f(0) với ∀ x ∈ (-1 ; 1) và x ≠ 0
⇒ Hàm số y = f(x) đạt cực tiểu tại x = 0.
Bài 4 (trang 18 SGK Giải tích 12):
Chứng minh rằng với mọi giá trị của tham số m, hàm số
y = x3 – mx2 – 2x + 1
luôn luôn có một cực đại và một điểm cực tiểu.
Lời giải:
TXĐ: D = R
+ y’ = 3x2 – 2mx – 2
y’ = 0 ⇔ 3x2 – 2mx – 2 = 0 ⇔ 
+ y’’ = 6x – 2m.
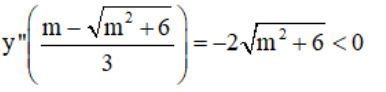
⇒ 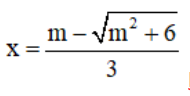 là một điểm cực đại của hàm số.
là một điểm cực đại của hàm số.

⇒ 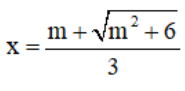 là một điểm cực tiểu của hàm số.
là một điểm cực tiểu của hàm số.
Vậy hàm số luôn có 1 điểm cực đại và 1 điểm cực tiểu.
Bài 5 (trang 18 SGK Giải tích 12):
Tìm a và b để các cực trị của hàm số
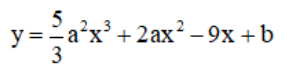
đều là nhưng số dương và xo = -5/9 là điểm cực đại.
Lời giải:
TXĐ: D = R.
+ y’ = 5a2x2 + 4ax – 9.
⇒ y’’ = 10a2x + 4a.
– Nếu a = 0 thì y’ = -9 < 0 với ∀ x ∈ R
⇒ Hàm số không có cực trị (loại)
– Nếu a ≠ 0.


Các cực trị của hàm số đều dương
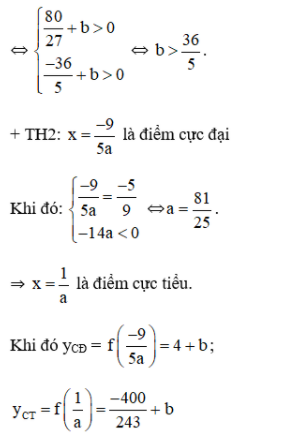
Các cực trị của hàm số đều dương
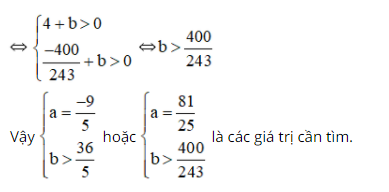
Bài 6 (trang 18 SGK Giải tích 12):
Xác định giá trị của tham số m để hàm số m để hàm số 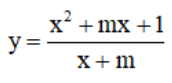 đạt giá trị cực đại tại x = 2.
đạt giá trị cực đại tại x = 2.
Lời giải:
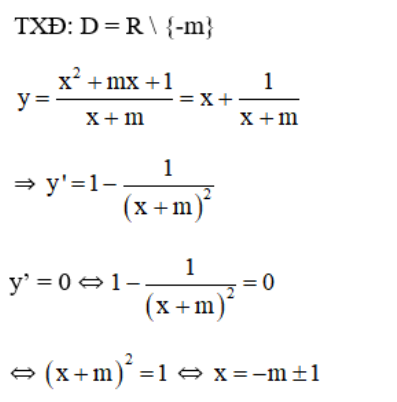
Ta có bảng biến thiên:
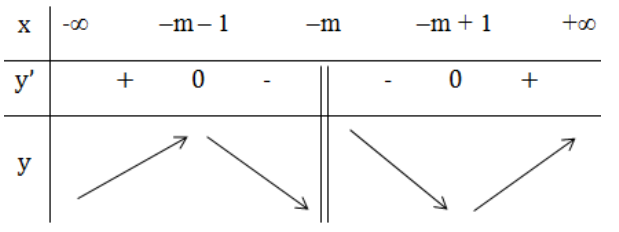
Dựa vào BBT thấy hàm số đạt cực đại tại x = -m – 1.
Hàm số đạt cực đại tại x = 2 ⇔ -m – 1 = 2 ⇔ m = -3.
Vậy m = -3.
Trên đây là nội dung liên quan đến Cực Trị Của Hàm Số – Toán 12 được dean2020.edu.vn đã tổng hợp được và chia sẻ đến các bạn. Hy vọng những kiến thức mà chúng tôi chia sẻ sẽ mang lại cho bạn những thông tin bổ ích nhé!
- Đỉnh Núi Fansipan – Những Điều Cần Lưu Ý Để Có Một Chuyến Đi Tuyệt Vời
- Nhà thơ T.T.Kh – Nhà thơ bí ẩn với những sáng tác đi vào lòng người
- Ngành công nghệ thực phẩm – Học ngành công nghệ thực phẩm ra trường làm gì ?
- Những Câu nói Thả Thính Hay đăng FB, Zalo, MXH bao chất
- MongoDB là gì? Những tính năng của MongoDB bạn nên biết