Để học tốt Hình Học 10, phần dưới giải các bài tập sách giáo khoa Toán 10 được biên soạn bám sát theo nội dung SGK Toán Hình Học 10. Dưới đây chúng ta sẽ cùng tìm hiểu nội dung Tích Vô Hướng Của Hai Vectơ – Toán 10 và giải một số bài tập liên quan đến nội dung này để nắm chắc kiến thức nhé!
I. Lý thuyết Tích vô hướng của hai vectơ
1. Định nghĩa
Cho hai vectơ ![]() đều khác vectơ
đều khác vectơ ![]() . Tích vô hướng của
. Tích vô hướng của ![]() là một số, kí hiệu là
là một số, kí hiệu là ![]() . được xác định bởi công thức sau:
. được xác định bởi công thức sau:
![]()
Trường hợp ít nhất một trong hai vectơ ![]() bằng vectơ
bằng vectơ ![]() ta quy ước:
ta quy ước:
![]()
Chú ý
+) Với ![]() khác vectơ
khác vectơ ![]() ta có:
ta có:
![]()
+) Khi ![]() tích vô hướng
tích vô hướng ![]() được kí hiệu là
được kí hiệu là ![]() và số này được gọi là bình phương vô hướng của vectơ
và số này được gọi là bình phương vô hướng của vectơ ![]()
Ta có:
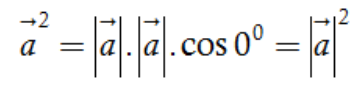
2. Các tính chất của tích vô hướng
Người ta chứng minh được các tính chất sau đây của tích vô hướng:

Nhận xét. Từ các tính chất của tích vô hướng của hai vectơ ta suy ra:
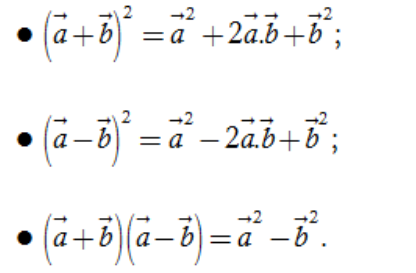
3. Biểu thức tọa độ của tích vô hướng
Trên mặt phẳng tọa độ 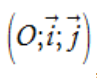 , cho hai vectơ:
, cho hai vectơ:
![]()
Khi đó tích vô hướng ![]()
![]()
Nhận xét. Hai vectơ:
![]()
đều khác vectơ ![]() vuông góc với nhau khi và chỉ khi: a1b1 + a2b2 = 0.
vuông góc với nhau khi và chỉ khi: a1b1 + a2b2 = 0.
4. Ứng dụng
a) Độ dài của vectơ
Độ dài của vectơ ![]() = (a1, a2), được tính theo công thức:
= (a1, a2), được tính theo công thức:
![]()
b) Góc giữa hai vectơ
Từ định nghĩa tích vô hướng của hai vectơ ta suy ra nếu ![]() = (a1, a2) và
= (a1, a2) và ![]() = (b1, b2) đều khác
= (b1, b2) đều khác ![]() thì ta có:
thì ta có:
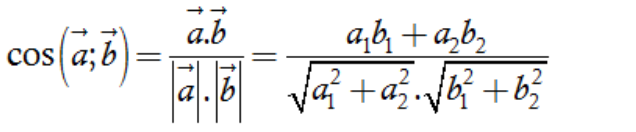
c) Khoảng cách giữa hai điểm
Khoảng cách giữa hai điểm A(xA; yA) và B(xB; yB) được tính theo công thức:
![]()
II. Giải Bài Tập SGK
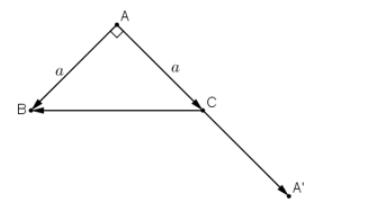
Bài 1 (trang 45 SGK Hình học 10):
Cho tam giác vuông cân ABC có AB = AC = a. Tính các tích vô hướng ![]()
Lời giải:

Bài 2 (trang 45 SGK Hình học 10):
Cho ba điểm O, A, B thẳng hàng và biết OA = a, OB = b. Tính tích vô hướng ![]() trong hai trường hợp:
trong hai trường hợp:
a) Điểm O nằm ngoài đoạn AB;
b) Điểm O nằm trong đoạn AB.
Lời giải:
a) Điểm O nằm ngoài đoạn AB :

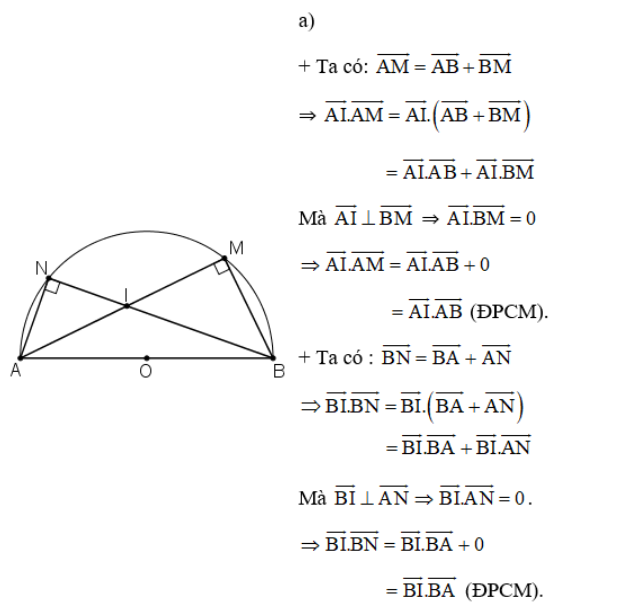
Bài 3 (trang 45 SGK Hình học 10):
Cho nửa hình tròn tâm O có đường kính AB=2R. Gọi M và N là hai điểm thuộc nửa đường tròn sao cho hai dây cung AM và BN cắt nhau tại I.
a) Chứng minh ![]()
b) Hãy dùng kết quả câu a) để tính ![]() theo R.
theo R.
Lời giải:

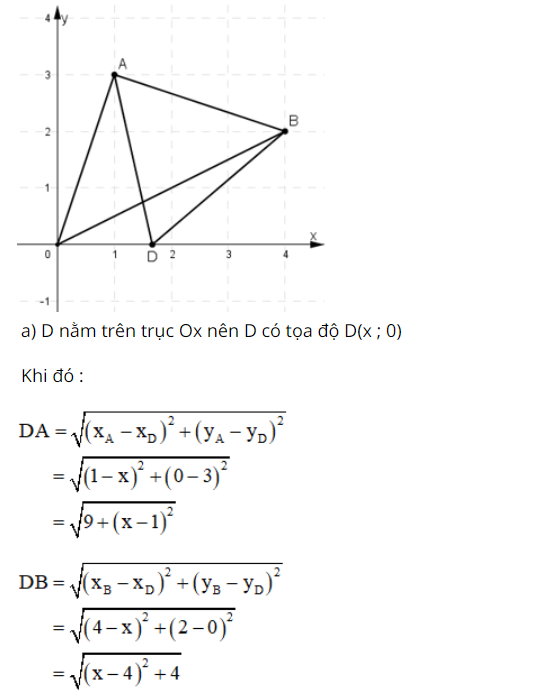
Bài 4 (trang 45 SGK Hình học 10):
Trên mặt phẳng Oxy, cho hai điểm A(1; 3), B(4; 2).
a) Tìm tọa độ điểm D nằm trên trục Ox sao cho DA = DB;
b) Tính chu vi tam giác OAB.
c) Chứng tỏ OA vuông góc với AB và từ đó tính diện tích tam giác OAB.
Lời giải:
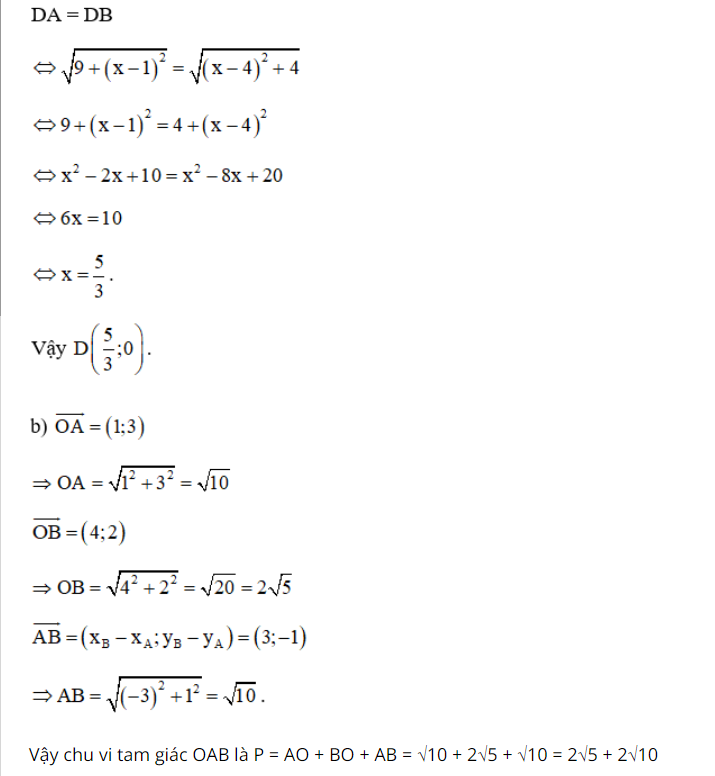
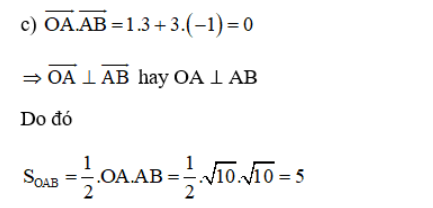
Bài 5 (trang 46 SGK Hình học 10):
Trên mặt phẳng Oxy hãy tính góc giữa hai vectơ a→ và b→ trong các trường hợp sau:
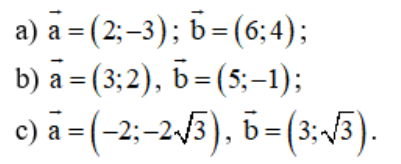
Lời giải:
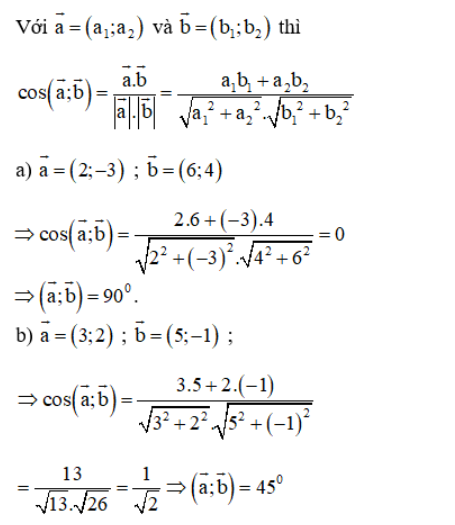
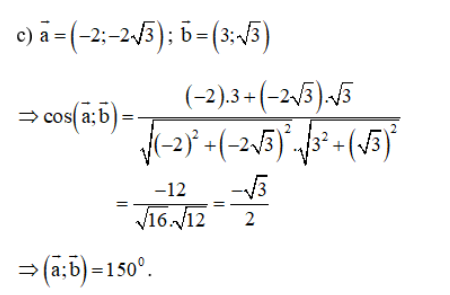
Bài 6 (trang 46 SGK Hình học 10):
Trên mặt phẳng tọa độ Oxy cho bốn điểm: A(7; -3), B(8; 4), C(1; 5), D(0; –2). Chứng minh rằng tứ giác ABCD là hình vuông.
Lời giải:

Trên đây là nội dung liên quan đến Tích Vô Hướng Của Hai Vectơ – Toán 10 được dean2020.edu.vn đã tổng hợp được và chia sẻ đến các bạn. Hy vọng những kiến thức mà chúng tôi chia sẻ sẽ mang lại cho bạn những thông tin bổ ích nhé!